Research Interests
My current research spans nonequilibrium physics, active matter, animal navigation, and machine learning. In my work, I use tools from statistical physics, nonlinear dynamics, and stochastic processes to tackle forward problems, predicting emergent dynamical states from microscopic rules. In particular, I have identified phase transitions in minimal nonequilibrium models, dynamical instabilities in active matter, and universal properties of active particles.
Beyond the classical forward approach, I also address inverse problems, exploring questions like: What is the optimal navigation strategy for an animal in a noisy environment? How can we manipulate the mechanical properties of an environment to determine the dynamical state of an active system? What are optimal protocols to efficiently train an artificial neural network? To answer these questions, I combine techniques such as dimensionality reduction and path-integral methods with optimal control theory. Below, I present some of these ideas.
Optimal Learning in Neural Networks
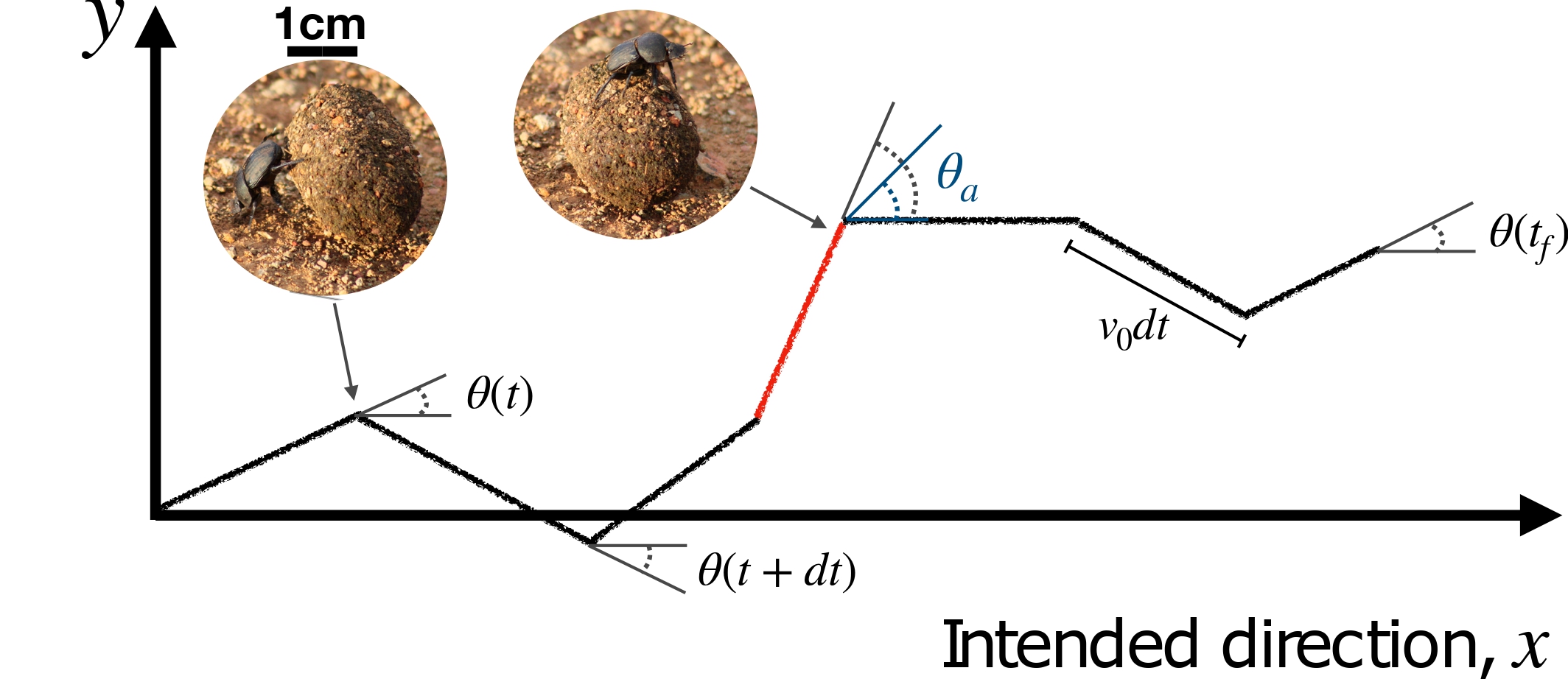
In machine learning, various optimization methods are introduced at different stages of the pipeline to improve performance. These include the dynamic selection of training examples and tasks (e.g., curriculum learning), adaptive hyperparameters (e.g., learning rate schedules), and dynamic architectures. While these strategies accelerate training, they often rely on trial-and-error heuristics that lack a theoretical foundation. A key challenge is that standard optimal control techniques, which could optimize these hyperparameters, are limited by the curse of dimensionality. At the same time, learning problems are inherently high-dimensional.
To bypass the curse of dimensionality, in my work, I use dimensionality reduction techniques from statistical physics, identifying reduced (but exact!) description of the learning process where optimal control can be directly applied. We have applied this idea to a variety of problems, including continual learning, curriculum learning, and dropout regularization. Many more exciting applications are to come!
Multimodal Animal Navigation
Similar challenges arise in biological systems, where animals continuously adapt their learning and navigation strategies to complex, dynamic environments. Like artificial systems, biological learners must acquire new knowledge over time while avoiding the loss of previously learned information. Moreover, they have to actively sense their environment to make decisions under uncertain conditions. In my work, I try to identifying learning and navigation principles, specifically on how to optimally combine multiple sources of information.
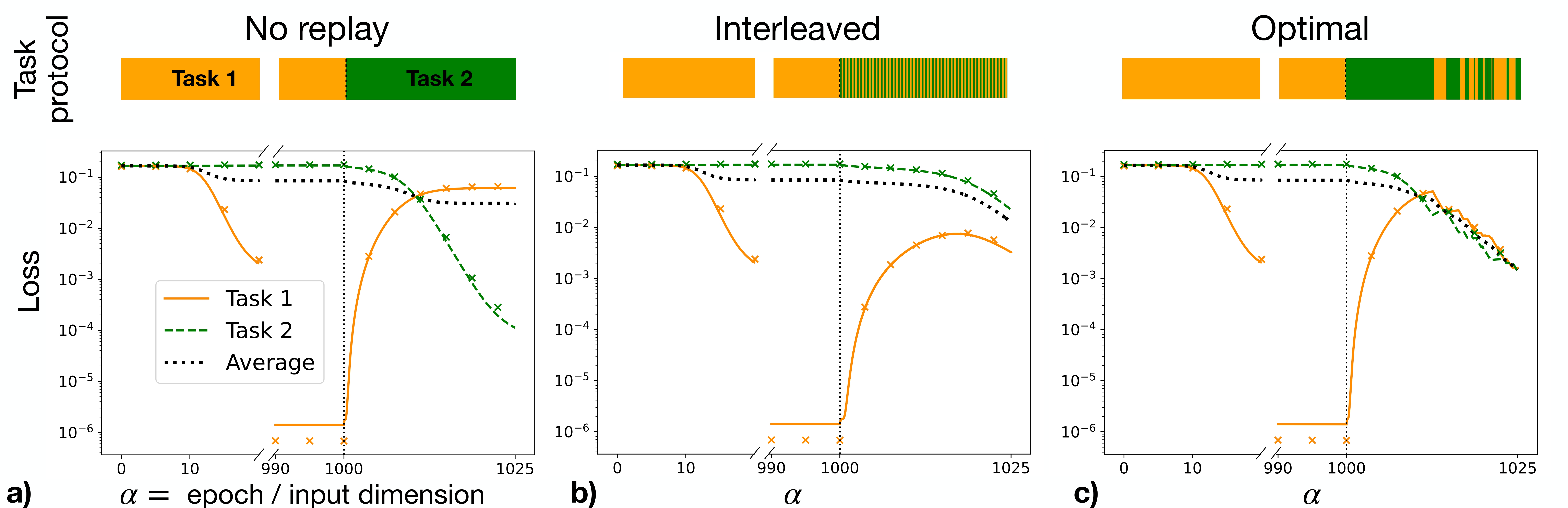
In collaboration with Prof. Mahadevan (Harvard), we applied this question to the well-studied rolling behavior of dung beetles (see video here), which use different sensory cues to orient. By modeling optimal switching strategies, we found that noisier environments favor more frequent reorientations, a result that may generalize to other multi-modal navigation systems.
Control of Active Materials
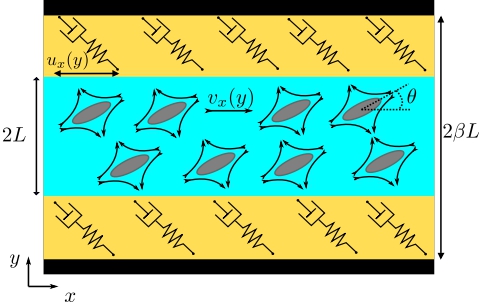
Active matter describes systems composed of units that are capable of converting energy from their environment into mechanical work. They are observed across scales, from swimming bacteria to the collective movement of birds. The local energy injection differentiates active from passive systems. As a result, active matter is driven away from thermal equilibrium, resulting in novel physical behaviors beyond standard equilibrium physics. In particular, dense active systems often result in spontaneous flows, that emerge without applying any pressure gradients. However, these flows are typically chaotic, and controlling them in space and time could enhance our understanding of self-organization in biological systems and offer insights into using active matter in functional materials.
In my work, I explored the control mechanisms in active matter systems by tuning the mechanical properties of the surrounding environments. In collaboration with the group of Prof. Yeomans (Oxford), we have shown that viscoelastic confinement produces coherent oscillations in active nematics.
Stochastic Thermodynamics
I am interested in quantifying irreversibility in nonequilibrium systems across different scales, with a focus on how concepts from stochastic thermodynamics and nonequilibrium statistical physics can help characterize learning processes in both biological and artificial systems.
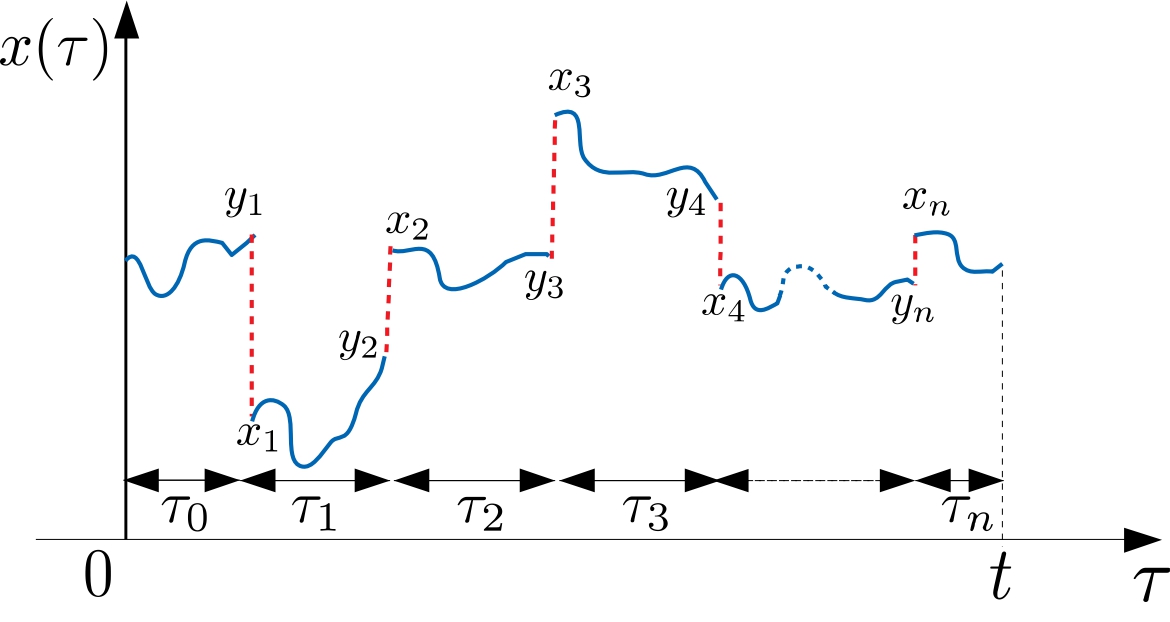
In my research on the stochastic thermodynamics of low-dimensional systems, I developed a path-decomposition method to derive the full distribution, including large deviations, of entropy production in a minimal model. This model involves a particle undergoing diffusion with intermittent restarts, and my work uncovered a nonequilibrium phase transition associated with rare trajectories that produce unusually high entropy.